Tko je u pravu? Psiholog, sa svojim studijama provođenim u laboratoriju, ili instruktor s bogatim iskustvom iz prakse? Kako su uopće uspjeli doći do potpuno suprotnih zaključaka? Možda će nam biti jasnije nakon drugog primjera.
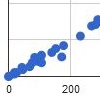
Zamislite se kako pokušavate dobiti što veće brojeve pri bacanju kocke. Kad vam padne jedinica iz očaja kocku tresnete o stol, kako bi ste okrenuli sreću i sljedeće bacanje bi dalo veći broj. Vaš suparnik ima suprotnu strategiju: on svoju kocku ljubi kad je dobio šesticu, u nadi da će je tako "nagraditi" i ponovo dobiti maksimalni broj bodova. Obojica bacate svoju kocku i bilježite koliko ste koji put dobili. Evo grafičkog prikaza nakon 100 takvih bacanja.
Čini da vaša strategija pomaže jer nakon tog rituala vrlo često dobijete bar dvojku. S druge strane, suparnikova strategija je potpuni promašaj — ljubljenje vrlo rijetko dovodi do ponovljene šestice. "Kažnjavanje" kocke funkcionira, "nagrađivanje" ne.
Ali, što ja pričam? Pa udaranje i ljubljenje kocke nema stvarnog utjecaja na ishod "igre". Simulirali smo potpuno slučajne brojeve, "kocka" nije osjetila nikakvu kaznu niti nagradu. Naša interpretacija rezultata je samo psihološka varka.
Razmislite: nakon što dobijete jedinicu, u pet od šest slučajeva sreća će vam se nasmiješiti i pasti će dvojka ili više. Nakon šestice, u pet od šest slučajeva sljedeće bacanje će dati manji broj. Svako bacanje je neovisno od prethodnih i kad god se "udaljimo" od prosjeka, sljedeće bacanje će biti sklonije da nas "povuče" u suprotnom smjeru.
Ovaj članak je dio serije članaka o varljivoj statistici:
Povratak prosjeku
Ovo je elementarna statistička zakonitost koja se naziva povratak srednjim vrijednostima (engleski regression toward the mean). U situacijama kad varijabla slučajno varira oko neke srednje vrijednosti, svaki put kad znatno odstupi od tog prosjeka povećava se i vjerojatnost da u sljedećem neće biti još ekstremnija.
Što se onda dogodilo pilotima s početka priče? Da demonstrira pogrešku instruktorima, Kahneman je organizirao natjecanje u gađanju nacrtane mete, u dva pokušaja. Zatim je rangirao instruktore po uspješnosti, za svaku "rundu" posebno. Instruktori su se mogli uvjeriti kako je većina onih koji su bili na vrhu rang liste u prvoj rundi pokvarila rezultat u drugom pokušaju, kao i da se većina onih koji su imali slab rezultat pri prvom pokušaju kasnije popravila — bez ikakvih pohvala i kažnjavanja.
Doduše, uspješno izvođenje manevara nije isto što i gađanje mete, a definitivno nije isto što i bacanje kocke. Pa ipak, to je vrlo složena vještina koju je teško konzistentno izvršavati i kod koje je slučaj nezanemariv faktor. Vještina pilota-kadeta s početka članka također je slučajno varirala oko nekog njihovog prosjeka. Iako se ta prosječna vještina kroz dulji period obuke sigurno napredovala, još uvijek je postojao značajan utjecaj sreće na njihov uspjeh od jednog do drugog leta. Lako je moguće da je neki izniman, dobro ili loše odrađen manevar mogao zahvaliti slučaju, (ne)sreći koja nije dugog vijeka. Kudili ga mi ili hvalili, vjerojatno sutra neće imati tako izniman dan, nego neki koji će biti bliži njegovoj prosječnoj razini vještine.
Slučajno poboljšanje
Ovaj princip možemo primijetiti i kod kroničnih bolesti. Puno ljudi su se uvjerili kako im pomažu metode koje u objektivnim testiranjima ne pokazuju učinkovitost. Efekt povratka srednjim vrijednostima može biti uzrok.
Naime, mnoge kronične bolesti imaju svoje bolje i lošije dane. Naše stanje se može popravljati i pogoršavati bez očitog razloga, i bez obzira što radili. No, budući da smo najskloniji pokušavanju nekih novih metoda kad se osjećamo naročito loše, nije neobično što nam se pukim slučajem stanje nakon toga poboljša. Stoga nam učinak povratka srednjim vrijednostima može dati lažni dojam da je ta metoda uzrok ozdravljenja. Dokle god metodu koristimo samo kad nam je iznadprosječno loše, za očekivati je da će nam nakon nje biti bolje, pukim slučajem.
A sad vi!
Evo dva primjera statističkih zanimljivosti iz svakodnevnog života. Možete li u njima prepoznati učinak povratka srednjim vrijednostima?
1. Natjecanje u skijaškim skokovima sastoji se od dva skoka. Skakač koji je prvi put iznimno daleko skočio u pravilu ostvaruje lošiji rezultat na drugom skoku. Možda je bio preopterećen pritiskom da očuva vodstvo? Natjecatelj koji je skočio ispod svojih mogućnosti obično popravlja svoj rezultat u drugom skoku; vjerojatno je opušteniji i smioniji jer zna kako nema što izgubiti. Ili možda postoji jednostavnije objašnjenje? (vidi objašnjenje)
Kao kod gađanja mete, i skijaški skokovi prirodno variraju u nepredvidljivom smjeru, tako da ovaj prepoznat uzorak vjerojatno ne treba dodatno objašnjavanje. No, ljudi imaju izraženu potrebu da šum u podacima pripišu ljudskim osobinama, željama i akcijama, umjesto da ih shvate kao slučajan ishod.
2. Američki časopis Sports Illustrated prati nesreća: sportaš koji završi na njihovoj naslovnici u sljedećoj sezoni se obično pogorša. Eto dokaza da sa slavom dolazi i pretjerano samopouzdanje i popuštanje discipline. Ili? (vidi objašnjenje)
Na naslovnici završavaju samo sportaši koji su bili iznimno uspješni te godine, a jedan od faktora uspjeha je i slučaj. Sljedeće godine je vjerojatnije da im taj faktor slučajnosti neće tako ići u prilog.
3. Činjenica je kako se visokointeligentne žene obično udaju za muškarce koji su manje inteligentni od njih. Zašto? Možda ne žele muža koji će ih zasjeniti? Ili možda nisu imali neki izbor, jer visokointeligentni muškarci ne žele ženu koja će im biti intelektualno ravna? (vidi objašnjenje)
Kvocijenti inteligencije supružnika jesu korelirani—inteligentnije žene su sklone udati se za inteligentnije muškarce—ali ta korelacija nije savršena. Nesavršenost ostavlja prostora za efekt povratka srednjim vrijednostima, po kojem je vjerojatnije da će muž visoko inteligentne žene biti iz velikog skupa manje inteligentnih muškaraca, nego iz malog skupa muškaraca koji su još inteligentniji od nje.