05.11.2012.
Elementarni stanični automati
Sjećate li se onih bilježnica na kvadratiće kakve smo koristili u školi? Na njima smo u trenucima dosade znali igrati križić-kružić, podmornicu i druge igre kojima se teže sjetiti ime. Pa, evo jedne igre koja bi se mogla igrati na takvom papiru. Počnite tako da u prvom retku neke kvadratiće (polja) zacrnite, a neke ostavite praznima — to nam je početno stanje. Sljedeći redak ćemo popuniti po ovom pravilu: svako polje ispod zacrnjenog neka sad ostane prazno, a svako polje ispod praznog sad zacrnite. Nakon par redaka dobijemo ovako nešto:
Ovaj članak koristi napredne mogućnosti browsera. Ako ne vidite grafiku gore ili primjećujete kako nešto ne radi dobro, pokušajte koristiti moderniji browser (Chrome, Firefox, IE9) i javite na kojem browseru ste imali problema.
OK, priznajem, ovo je prilično blesava igra. Treći red je opet isti kao onaj od kojeg smo krenuli. Stvar je u tome da s tako jednostavnim pravilom, prema kojem boja polja u sljedećem retku ovisi samo jednom polju iz prethodnog retka, niti ne možemo dobiti zanimljivije ponašanje.
Pogledajmo zato malo kompliciranija pravila, ona po kojima boja novog polja ovisi o tri polja iz prethodnog retka: osim o polju iznad, sad će ovisiti i o onima koji su dijagonalno gore lijevo i desno. Budući da neka tri polja mogu biti obojena na ukupno 23 = 8 načina, za svaku od tih kombinacija možemo definirati kojom će bojom (crnom ili bijelom) rezultirati polje u novom retku.
Uzmimo za primjer pravilo: "polje ispod oboji ako i samo ako je barem jedan od tri polja iznad njega obojen". Grafički ga možemo predstaviti tako da ispod svake moguće kombinacije tri polja prethodnog retka nacrtamo koje boje će biti rezultirajuće polje iz novog retka. U našem slučaju, svaka kombinacija rezultira crnim poljem, osim ako su sve tri polja bijela:
Ovakva pravila, koja se u matematici nazivaju elementarnim staničnim automatima, mogu se definirati s osam bitova informacije. Pravila ima točno 256, a svaki od njih se zove prema broju od 0 do 255 koji ti bitovi predstavljaju u binarnom sustavu. Ovaj naš automat ima jedinicu (crno polje) na svim mjestima osim zadnjeg, pa se tako naziva "Pravilo 254".
OK! Sad razmislite, kako će se takvo pravilo razvijati iz jedne crne točke na sredini papira? Budući da je "domet" pravila tek jedno polje ulijevo ili udesno, originalna "mrlja" odnosno bilo kakva informacija na mreži se može širiti brzinom od jednog polja po retku.
Prilično jednostavno. No, unatoč svojoj jednostavnosti, takvi automati mogu pokazati vrlo složeno ponašanje. Na primjer, prethodno pravilo promijenimo samo u prvoj kombinaciji tako da tri crna polja sad daju bijelo polje (pravilo 126).
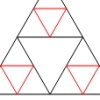
Izgleda vam poznato? Pogledajte veću sliku nadesno: to je upravo trokut Sierpinskog o kojem smo pričali prošli put. Pređite mišem preko slike. Za svako polje su označena tri polja iz prethodnog retka na temelju kojih je izračunata boja polja ispod strelice, kao i dio pravila koji definira to ponašanje.
I neki drugi elementarni stanični automati daju isti rekurzivni uzorak. Kliknite na neke primjere automata koji rezultiraju sierpinskijevskim uzorkom, ili eksperimentirajte sami klikom na pojedina polja u grafičkoj definiciji pravila da bi ga promijenili.
Pravilo 126 | Pravilo 18 | Pravilo 60 | Pravilo 62
Počevši od jedne točke, neka pravila daju predvidljive uzorke (iako su možda rekurzivni). No, neka od ovih pravila generiraju i nepredvidljive, kaotične uzorke. Pogledajte recimo Pravilo 30. Ne izgleda baš pravilno? Možda samo uz lijevi rub? Evo kako se pravilo razvija iz jedne točke u 250 redaka:

Trokut ima dosta šuma, no lijeva strana trokuta pokazuje određenu pravilnost: različiti uzorci se periodički ponavljaju, usporedno s lijevim rubom. Desna strana trokuta je bitno drugačija i u njoj nećete primijetiti ponavljanje i pravilnosti: primjećujete puno obrnutih trokuta raznih veličina, razbacanih unaokolo bez očitog smisla. Granica između reda na lijevoj strani i kaosa na desnoj je također nepravilna: spušta se od vrha trokuta vrludajući nepredvidljivo s lijeva na desno.
Četiri klase ponašanja
Ponašanje ovih elementarnih automata detaljno je opisao Stephen Wolfram u svojoj knjizi A New Kind of Science. Proučavajući razvoj stanica iz različitih, slučajno generiranih početnih stanja, automate je podijelio u četiri klase.
Kod automata klase 1, ponašanje je vrlo jednostavno i gotovo svi početni uvjeti vode do konačnog stanja koje se više ne mijenja. Npr. Pravilo 0 će jednostavno rezultirati bijelim papirom već u drugom koraku. Pravilo 250 će trebati više koraka, ali će na kraju sva polja biti crna.
Automati klase 2 vode do različitih mogućih konačnih stanja, ali svi oni se sastoje od jednostavnih struktura koje se više ne mijenjaju, ili se samo ponavljaju unutar nekoliko koraka. Vidi Pravilo 108 ili Pravilo 88.
Ponašanje automata klase 3 je složenije i čini se kaotično. Vidjeli smo kako Pravilo 30 može "izgenerirati" šum iz samo jedne točke. Drugačija početna stanja — bila ona i sama nepravilna i nasumična, ili vrlo jednostavna i pravilna — također generiraju takvo kaotično ponašanje.
Automati četvrte klase pokazuju najzanimljivije ponašanje. U njihovom ponašanju vidimo mješavinu uređenosti i slučajnosti: postoje lokalne strukture koje su same po sebi relativno jednostavne, ali putuju i stupaju u složene interakcije s drugim takvim strukturama.

Možda najzanimljiviji automat koji pokazuje ponašanje četvrte klase je Pravilo 110. Kao što možete vidjeti na slici, ono se od početne točke širi samo nalijevo. Ovo pravilo je manje kaotično: lijevi rub krase pravilno ponavljajući uzorci koji u pravilnim razmacima "šalju" dijagonalne crte prema desnom rubu. Uz desni rub se spušta nekakva nepravilna, ali stabilna struktura koja se ne ponavlja.
Ovaj sustav savršeno balansira između dosadne predvidljivosti automata prve i druge klase s jedne strane, te neuređenosti i konfuzije automata treće klase. Nedavno je matematički dokazano kako je ponašanje Pravila 110 dovoljno kompleksno da može (u načelu) simulirati rad bilo kojeg računala: moguće je kreirati takvo početno stanje da se nakon nekog broja koraka Pravila 110 dobiju nova stanja koja se mogu interpretirati kao točan rezultat simulacije odnosno izračuna. Pravila za kreiranje početnog stanja i ispravnu interpretaciju rezultata su, doduše, jako komplicirana, tako da ovo svojstvo Pravila 110 nema baš neku praktičnu vrijednost.
Što to sve znači?
Ovakvi automati se nazivaju elementarnima zato što su krajnje jednostavni: svako polje može imati samo dva moguća stanja, polja su raspoređena samo u jednoj prostornoj dimenziji (retke/korake promatramo kao promjenu kroz vrijeme), i pravila su definirana tako da jedno polje može utjecati samo na najbliže susjede u jednom koraku. No čak i tako ograničeni sustavi mogu iz praktički ničega stvarati vrlo kompleksno ponašanje: ponavljajuće uzorke, fraktale, deterministički kaos i strukture dovoljne kompleksnosti da se njima može simulirati bilo kakvo računalo. Pazite, ne neko računalo; bilo kakvo računalo, program, algoritam, obračun, čisti teorijski ili praktično implementiran, koji su ljudi dosad uspjeli smisliti.
To nam govori da i kompleksnost i nered ne mora dolaziti "izvana". Sušta jednostavnost može biti dovoljna da nastane proizvoljno velika kompleksnost; savršen red je dostatan da nastane proizvoljno neuređen kaos. Intuitivno nam se čini da složeno ponašanje treba imati složen uzrok, kompliciran sustav ili inteligentan dizajn u pozadini — no, ponekad naše intuicije spektakularno pogriješe.