22.04.2012.
Pogađanje pravila
Želite li probati jednu igru? Ide ovako: ja zamislim jedno jednostavno pravilo vezano uz niz brojeva — na primjer, pravilo može biti ovo "svaki sljedeći broj je manji za jedan". Zatim, vi napišete niz od neka tri broja, a ja ću za svaki dani niz odgovoriti s ✔ kad niz zadovoljava zamišljeno pravilo, ili s ✖ ako ga ne zadovoljava. U ovom slučaju, niz 3, 2, 1 bi zadovoljavao pravilo, a niz 6, 5, 3 ne bi. Cilj je da pogodite moje pravilo samo na temelju informacija o tome koji brojevi zadovoljavaju pravilo a koji ne.
Sad vi! Zamislio sam jedno jednostavno pravilo, opisano kratkom frazom. Pokušajte pogoditi koje je točno to pravilo na temelju testiranja koje ćete sami provesti. Evo jednog niza koji zadovoljava ovo pravilo:
✔
Pokušajte sami: upišite tri broja i kliknite na upitnik da biste saznali da li taj niz zadovoljava pravilo.
Molim unesite tri prirodna broja
Ponovite test koliko želite puta, s različitim nizovima brojeva. Nakon što ste se uvjerili da možete sa sigurnošću zaključiti po kojem pravilu se brojevi provjeravaju, kliknite na sljedeći gumb:
(Ovi nije trik pitanje. Pravilo koje tražite je vrlo jednostavno, svaki osnovnoškolac bi ga razumio. Poanta ove pitalice je da dođete do pravila onakvog kakvog sam ja zamislio, to jest bilo kakvog matematički ekvivalentnog oblika koji bi dao iste odgovore kad ga se testira.)
Jeste li sigurni da ste dovoljno testirali svoju ideju? Slobodno možete probati još par nizova, za svaki slučaj.
Dobro, evo pravila:
Rastući niz brojeva.
Jeste li ga pogodili?
U ovom klasičnom eksperimentu većina ljudi je mislila da je pravilo specifičnije. Nekima se na temelju prvog primjera učinilo kako je pravilo "uzastopni parni brojevi". Kad su pokušali testirati to pravilo (hipotezu), uglavnom su upisivali brojeve za koje su očekivali da će zadovoljiti to pravilo ("6 8 10", "20 22 24", itd.) i svaki put su potvrdili svoju tezu. Međutim, malo ljudi pokušava opovrgnuti svoju inicijalnu ideju testovima koji bi trebali pasti. "1 3 5" ne bi smjelo proći ako je pravilo stvarno "uzastopni parni brojevi" - ali u ovom slučaju prolazi.
Ako se teorija ne slaže s eksperimentom, onda je teorija kriva. Ako smo očekivali kako će proći samo uzastopni parni brojevi, a ispostavilo se da prolaze i neparni. Naša ideja je kriva, moramo je proširiti da obuhvaća i novu informaciju.
Međutim, ljudi imaju urođenu tendenciju da ne pokušavaju opovrgnuti postojeće mišljenje, nego ga samo pokušavaju potvrditi. To rade tako da nesvjesno preferiraju i traže informacije koje idu u prilog originalnom mišljenju, ili ih interpretiraju na pristran način. Ovaj efekt u stručnoj literaturi se naziva confirmation bias, što se može prevesti kao sklonost potvrdi.
Dokazi i opovrgavanja
Originalni "2-4-6" problem je namjerno napravljen tako da se traži pravilo koje je vrlo općenito, općenitije nego što sugerira prvi primjer. To nije jedina moguća konfiguracija.

Pogledajte dijagram desno. Testnih slučajevi (nizova od tri broja) su prikazani u pravokutnicima. Jedan dio njih zadovoljava traženo pravilo da niz bude rastući, i taj skup je predstavljen zelenim krugom. Svaki test unutar tog skupa ima pozitivan rezultat (✔), a svaki izvan njega negativan rezultat (✖). Dokle god dobivamo pozitivne rezultate za pozitivan test (pozitivan test je onaj koji bi prema hipotezi trebao imati pozitivan rezultat) i negativne rezultate za negativan test (onaj koji po hipotezi ne bi trebao zadovoljiti pravilo), potvrđivat ćemo da je naša hipoteza ispravna.
Međutim, ograničen broj uspješnih testova (zeleni pravokutnici na slici) ne može dokazati hipotezu. Jedini način da budemo potpuno sigurni da je pravilo pogođeno je da ispitamo sve moguće slučajeve — što je u praksi neizvedivo. Stoga se fokusiramo na pokušaje da je oborimo. Što smo bolji u svojim napadima i što hipoteza dulje odolijeva, možemo biti sigurniji u to da je stvarno točna.

U našem slučaju ljudima padaju na pamet hipoteze koje su podskup pravog pravila, i stoga će svaki pozitivan test imati pozitivan ishod. Recimo da testiramo hipotezu da je traženo pravilo "uzastopni parni brojevi" (hipoteze su na dijagramu označene crvenim krugom). Budući da je svaki niz uzastopnih parnih brojeva ("4 6 8" ili "18 20 22") ujedno i rastući niz, pozitivni testovi ne nam neće pomoći otkriti da je hipoteza prespecifična. Jedina je vrsta testa koja bi nam mogla dati konačnu odluku u tom slučaju—da hipoteza ne stoji—je negativan test. Većina negativnih testova za ovu hipotezu (npr. "3 2 2") će imati negativan rezultat i zato neće ukazati na pogrešnu hipotezu. Tek kad negativan test da pozitivan rezultat (u ovom slučaju će to dati bilo koji rastući niz koji ne čine uzastopni parni brojevi), znat ćemo da je hipoteza kriva. (Test koji opovrgava hipotezu je na dijagramu označen crvenim pravokutnikom.)
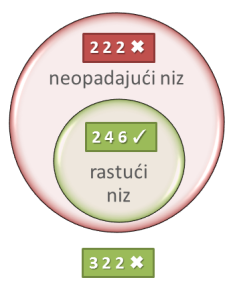
S druge strane, da smo testirali hipotezu koja je još općenitija od traženog pravila negativni testovi nam ne bi pomogli. Pogledajte dijagram lijevo. Na primjer, za hipotezu "neopadajući brojevi" negativan test poput "3 3 2" je ujedno i negativan test traženog pravila, pa će svaki negativan test imati očekivan negativan rezultat. U ovoj konfiguraciji, jedino pozitivni testovi bi mogli dokazati da to pravilo ne stoji, ako odaberemo neki niz koji je neopadajući a nije ni strogo rastući (npr. "3 3 3").
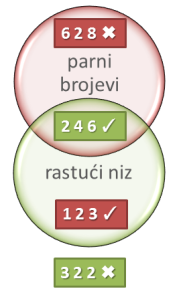
Treći slučaj je najopćenitiji (dijagram desno): niti traženo pravilo ni naša hipoteza nisu jedni drugome nadskup. Skupovi moraju imati neko preklapanje, jer da oba zadovoljavaju početni test "2 4 6". Primjerice, hipotezu "parni brojevi" mogu opovrgnuti i neki pozitivni (npr. "6 2 8") i neki negativni testovi (npr. "1 2 3"). S druge strane, i pozitivni i negativni testovi mogu potvrditi hipotezu.
Zaključak
Iz svih ovih primjera možete vidjeti kako je za dolaženje do ispravne slike stvarnosti na temelju ograničene mogućnosti testiranja potrebno koristiti dva neintuitivna pravila:
- Kako bi se uvjerili da smo u pravu trebamo što je moguće jače pokušati dokazati da smo u krivu. Umjesto da samo tražite primjere koji potvrđuju vašu hipotezu, pokušajte je opovrgnuti.
- Kako bi opovrgnuli hipotezu morate koristiti i pozitivne i negativne testove.
No, zašto ova pravila zvuče neintuitivno? Zašto su ljudi skloni potvrđivanju svojih ideja, kad opovrgavanje nosi kvalitetnije znanje?
Smatra se kako je razmišljanje u terminima potvrđivanja ljudima draže jer je mentalno lakše. Ono slijedi postojeći tok misli i učvršćuje ga, dok nas otkrivanje opovrgavajućih dokaza tjera da revidiramo naše razmišljanje i uložimo dodatan mentalni trud. A izgleda i da nitko ne voli doći do zaključka da je bio u krivu.




